Il s'agit d'un terme assez courant en imagerie médicale, sans que sa signification soit toujours claire. Commençons par un peu d'étymologie : ce terme vient du grec "τομος", la coupe, et de "γραφω", écrire (je ne me souviens plus exactement de mes déclinaisons en grec ancien, mais bon, je fais confiance à la littérature là-dessus). Cela veut dire qu'une tomographie permet de réaliser des images par coupes, par tranche. Mais cette définition s'applique quasiment à toutes les méthodes d'imagerie médicale... Initialement, on a utilisé le terme pour la reconstruction des image utilisant le procédé de "transformée de Radon". Il a notamment été beaucoup utilisée pour la tomodensitométrie (ou CT-scan, pour "Computed Tomography scanner").
Cette dernière technique est basée sur la radiographie. Dans cette dernière, on émet des rayons X à travers le corps d'un patient. Ceux qui ne sont pas absorbés par les organes sont transmis à travers le patient en ligne droite et sont absorbés par une plaque placée derrière celui-ci. Cette plaque, transparente à la base, s'assombrit lorsque des rayons X l'atteignent : on obtient ainsi une sorte de négatif de photographie, avec des zones plus ou moins transparentes selon la quantité de rayons absorbés. Les procédés actuels utilisent des capteurs électroniques plutôt qu'une plaque de photographie, mais le principe est identique.
La radiographie obtenue est une image à deux dimensions. Si cette image est suffisante dans de nombreux cas, comme la détection d'une fracture simple, elle ne permet pas toujours de localiser précisément des pathologies. Par exemple, on ne peut pas faire la différence entre un tissu mince et très absorbant et un tissu deux fois plus épais et deux fois moins absorbant. On peut réaliser d'autres images avec d'autres angles, mais ce n'est pas forcément suffisant.
Une solution au problème a été apportée au début du XXe siècle par un Autrichien nommé Johann Radon - rien à voir avec l'élément chimique radioactif du même nom. Celui-ci a proposé une opération mathématique qui porte maintenant son nom, la "transformée de Radon". Celle-ci dit que si l'on calcule la projection d'une forme dans chaque position et dans chaque direction, on obtient un ensemble de nombres que l'on peut ranger dans un tableau - que l'on appelle sinogramme. Puis, avec la transformée de Fourier inverse, une opération mathématique bien connue des physiciens, on peut reconstruire une image à deux dimensions de la forme initiale. Le lien avec le problème précédent ? C'est qu'avec des radiographies réalisées à différents angles, c'est comme si l'on avait des projections à différentes positions et angles ! Même si cette technique nécessite en théorie une infinité de radiographies et d'angles, ce qui serait très long en pratique, on l'utilise avec quelques astuces pour faire de la tomodensitométrie, c'est à dire former des images à trois dimensions, dans les scanners à rayons X.
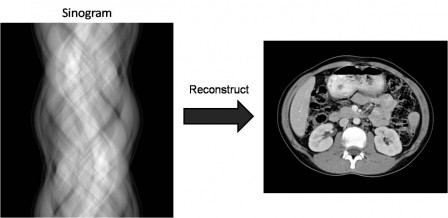
Depuis, d'autres algorithmes, basés sur des simulations, ont vu le jour. Ils nécessitent un modèle sur le milieu à reconstruire - on suppose que l'on va faire une image d'un coeur, de poumons, d'os, ce qui devrait donner ce genre d'image - et fonctionnent de manière itérative : chaque résultat de simulation permet d'améliorer le modèle, ce qui donne un nouveau résultat, qui permet d'améliorer le modèle, etc. Ces méthodes et celles basées sur la transformée de Radon donnent des résultats différents, et le débat pour savoir quelle est la "meilleure" technique n'est toujours pas résolu.

Le principe de la tomographie a été repris dans d'autres techniques, comme la Tomographie par Emission de Positon et la Tomographie d'Emission MonoPhotonique. Les scientifiques ont par la suite développé d'autres techniques comme la Tomographie d'Impédance Electrique, mais celles-ci n'utilisent pas de transformée de Radon !
Références
- Un article présentant une technique de reconstruction tomographique basée sur la transformée de Radon
- Le livre de Kak et Slaney qui fait référence, pour savoir tout, tout, tout sur la tomographie !
- Si vous avez Matlab, il y a une fonction toute prête pour faire des tomographies avec des transformées de radon, notamment radon et iradon




